CIS 1.5 Science Section

Brooklyn College

Professor Langsam

 

Assignment #4[1]

 

An ideal gas is defined as a gas which follows the equation

 

                                                                                                                 

                                                                                                                                             

 

 

Where P = pressure (in atm), V = volume (in liters), n = the number of moles, R is a constant (0.0821 liter-mole/atm-deg), and T is the temperature (in degrees Kelvin). An ideal gas assumes

  1. Gasses consist of molecules in constant random motion.
  2. The molecules exert no forces of attraction or repulsion upon one another.
  3. Molecular collisions are elastic that is. No kinetic energy is lost during a collision.
  4. The molecules are negligibly small compared to the volume of their container.

 

However, for real gasses at conditions of high pressure and temperatures, the actual behavior of a gas may be described by the Van der Waals Equation

 

                                                                                        

 

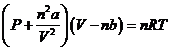
where a and b are experimentally determined constants for each gas that “correct” the observed pressure and the observed volume of a real gas to those of an ideal gas (see the table below).

 

gas

a

b

He

0.0341

0.0237

H2

0.244

0.0266

O2

1.36

0.0318

CO2

3.59

0.0427

H2O

5.46

0.0305

 

 

Write a program that will compare the pressures of a “real gas” with an ideal gas over a range of temperatures. Assume 1 mole of a gas in a 1 liter container and have the temperature vary from 100°K to 500°K in increments of 25 degrees. Calculate the % error of the ideal gas equation for each data point. The % error may be calculated by

 

                                                                              

 

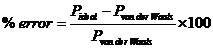
Repeat the calculation for each of the gasses in the table.

 

Strategy

 

  1. Solve each of the equations algebraically for P.
  2. Write functions idealPressure, vanDerWaalsPressure, and percentError.
  3. Write a function readConstants to read the gas, and the constants a and b from a data file vanDerWaalsConstants.dat (use the data presented in the table above), one set at a time.
  4. The main function  calls readConstants until there is no more data, and uses a for‑loop to repeatedly call the functions you wrote in step 2 for each temperature.

 

 

All output is to be to a file. Be sure you program is neatly structured, well commented and uses meaningful variables. Submit your source code, and both input and output files.

 


[1] Dillard and Goldberg, Chemistry: Reactions, Structures, and Properties, Macmillan, 1971