 C.I.S. 1.5 (Science Section)
C.I.S. 1.5 (Science Section)
Professor Langsam
Assignment #1 – Wheeled Robots
In order to control wheeled robots, it is necessary to understand the relationship between the forward linear motion of the object on the wheels and the rotation of the wheels.
When a wheel rotates, its circumference is in contact with the ground and it is assumed that it does not slip. Note that the wheel’s center of rotation is directly above the point of contact with the ground. Therefore, whatever distance the circumference of the wheel covers, that is precisely the distance covered by the center of rotation of the wheel (see Figure 1).
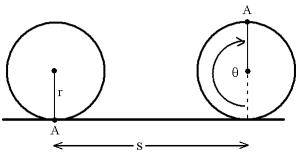
Figure 1
So, if a wheel makes one revolution (360° = 2p), then its center will move one circumference. The circumference of a circle C is related to its radius by a simple formula:
![]()
Thus a wheel of radius R will move a distance C for every revolution of the wheel. The bigger the radius, the greater the distance covered per revolution. If a motor turns a wheel at a fixed angular rate (revolutions per second), a bigger wheel will move forward at a faster rate.
Angles are usually measured in degrees or in radians. An angle of 360° (or one complete revolution) is equivalent to 2p radians. (A radian is a unit-less quantity.) Therefore, angular velocity can be specified in:
- Revolutions per second (rev/sec)
- Degrees per second (° /s) or
- Radians per second (s-1) (inverse seconds).
The forward distance moved by a wheel s (meters), is related to the angular rotation φ (radians) by:
![]()
And the relationship between rotation velocity, ω, and linear velocity of a wheel is given by:
![]()
where ν is given in meters/sec, ω is given in radians/sec, and R is in meters.
Write a C++ program that calculates the distance (s) and velocity (ν) of a wheeled robot traveling for t seconds, given various wheel sizes (R) and angular velocities (φ).
For each set of data your program should print a message such as:
FOR A ROBOT HAVING WHEELS OF RADIUS _______ METERS, AND AN ANGULAR RATE OF _______ REVOLUTIONS PER SECOND TRAVELING FOR _______ SECONDS, THE DISTANCE TRAVELED IS ______ METERS AND THE VELOCITY IS _____ METERS PER SECOND.
Calculate the above for the following sets of data:
|
Wheel Radius |
Angular Rate |
Time |
|
.02 |
1 |
5 |
|
.02 |
5 |
5 |
|
.02 |
10 |
5 |
|
.04 |
1 |
5 |
|
.04 |
5 |
5 |
|
.04 |
10 |
5 |
Use the trailer method to signal the end of the data. Be sure to use meaningful variables, comment your program, and use a consistent style.
Sample Calculation
Assume:
R = .05 meter
ω = 10 revolutions/second
t = 5
seconds
p = 3.14
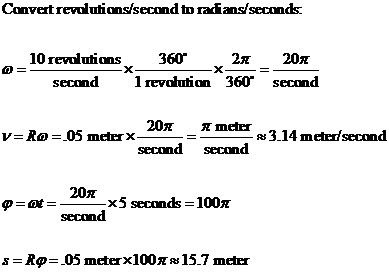
.