C.I.S. 1.5 (Science Section)

Brooklyn College

Professor Langsam

Assignment #1

A torus is a solid of revolution. It is formed by rotating a circle about a line that is in the plane of the circle, but not intersecting the circle. A torus has the shape of a doughnut.

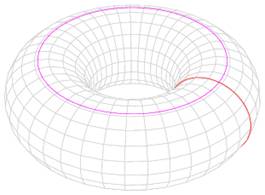
Let r be the radius of the tube and R the distance from the center of the torus to the center of the tube, its volume (useful for calculating the number of calories) and its surface area (useful for calculating the amount of glaze necessary to cover its surface), may be calculated as follows:

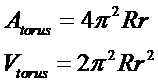
Now the radius of the hole is given by R-r, thus the area of the hole may be calculated by the well known formula for the area of a circle:

Write a program to calculate the volume and surface area of a torus as well as the area of its hole, for the following sets of data (in cm):

r R

1.0 4.0

0.5 1.5

0.5 4.0

5.0 10.0

1.0 10.0

. .

. . make up 5 additional sets

. .

For each torus, print the following message:

When the radius of the torus (R) is ____ cm and the radius of the tube (r) is ____ cm the volume of a torus is _____ cm squared and its surface area is _____cc. The area of the hole is _____ cm squared.

Use the trailer method to signal the end of the data. Be sure to use meaningful variables, comment your program, and use a consistent style.